-
Je suis étonné du comportement des gens autour de moi, face à l’épidémie de coronavirus. Certes, beaucoup sont calmes et prudents, mais beaucoup sont, soit très négligents, (surtout des jeunes), croyant qu’ils ne risquent rien et que la contamination sera pour les autres, soit ils sont paniqués (surtout des personnes âgées), et ont souvent un excès de précautions, qui rend la vie impossible.
Certains jeunes font même preuve d’un égoïsme et d’une bêtise remarquable, comme ceux qui sont venus, puis repartis dans toute la France, à une rêve-party, qui a duré 3 jours et où ils étaient les uns sur les autres à danser dans un champ. Ils peuvent avoir disséminé le microbe dans tout le pays, comme l’avaient fait les évangélistes de Mulhouse, qui ont payé un lourd tribu (27 morts), mais qui ne pouvaient savoir, à l’époque, le danger du virus. Aujourd’hui personne n’ignore et un tel comportement est donc criminel, car des gens risquent d’en mourir. En fait ce sont des comportements de gens inintelligents qui se croient immunisés et impunis, ou qui, incapables de prévoir et de réfléchir aux conséquences de leurs actes, ne se sentent pas responsables.
Les gens paniqués, leur comportement est plus naturel. Ce sont des gens le plus souvent pessimistes, anxieux, et qui n’ont pas l’habitude de prévoir et de réagir contre l’adversité. Ils ont du mal à évaluer le danger, et manifestent une prudence contre-productive. Le virus est pour eux une inconnue et ils sont paniqués face à une incertitude qu’ils ne supportent pas.
Savoir résister à la panique et sauver sa vie et celle des autres, voilà ce que savent faire les personnels soignants, qui ne fuient pas la réalité, mais, avec beaucoup de dévouement, ont le courage de l’affronter.Ces derniers temps j’ai constaté que de moins en moins de gens mettaient un masque dans l’hypermarché où je vais faire mes courses tous les jeudis matins. C’est regrettable, et curieusement, c’étaient le cas de très peu de femmes et la plupart du temps de personnes de moins de 30 ans. Probablement parce qu’ils croient que le virus ne touche pas les jeunes. C’est vrai qu’il y a moins de cas graves, mais je connais malheureusement un garçon de 23 ans qui est mort du covid19 et pourtant ce n’était pas une personne à risques.
Le gouvernement a enfin compris qu’il fallait imposer de mettre des masques dans des lieux clos. Mais je trouve qu’il n’a pas bien expliqué pourquoi et je voudrais donc expliquer la nécessité impérieuse de mettre un masque dans les espaces clos.
Voici d’abord la simulation de la quinte de toux d’une personne, qui se trouve entre deux murs, mais sans toit et qui, ne protégeant pas sa bouche, expulse des gouttelettes devant elle. Deux photos successives montrent la dissémination du nuage de gouttes, (diamètre entre 10 et 100 µ - millième de mm, en bleu), qui retombent assez vite et près et d’aérosols (diamètre inférieur au µ, en vert), qui peuvent même franchir le mur et persistent plusieurs minutes et parcourent une dizaine de mètres.
Voici ensuite la photo d’un éternuement, en cinéma ultra-rapide et la reconstitution du nuage, où là aussi les gouttes tombent à moins d’un mètre, mais les aérosols poursuivent leur route à ⅘ mètres.
Voici enfin deux photos de quelqu’un qui parle et la simulation de la dissémination de l’aérosol dans la pièce où discutent les personnes. en deux photos successives. Les particules rouges les plus petites (< 0,1 µ) iront ensuite dans toute le pièce et y resteront plus de 10 minutes.
A titre indicatif un éternuement dissémine environ 40 000 gouttelettes, une toux de 3.000 à 30 000 selon sa durée, et la parole 3.000 à 5 000 micro-gouttelettes en 5 minutes.
S’il n’y avait pas de phénomène d’évaporation ou de courants d’air, mais uniquement la pesanteur, une goutte de 100 µ tombe en environ 7 S, une de 10 µ de l’ordre de 17 mn et de 1µ, plus d’une quinzaine d’heures.Certes ce sont surtout les gouttelettes qui transportent des virus, et les micro-gouttes d’aérosols ne seront pas toutes contaminées et transporteront très peu de virus, mais elles peuvent cependant entraîner une contamination, si on les respire.
Il en résulte que, dans un espace clos, la distance de 1mètre n’est pas une garantie de sécurité.Alors à quoi sert le masque :
Certes si vous portez un masque il n’arrêtera peut être pas toutes les gouttelettes et notamment les aérosols, si quelqu’un vous éternue devant votre visage, mais dans les autres cas, il sera quand mêe relativement efficace
Mais surtout le masque se trouvant devant le nez et la bouche d’un éventuel contaminant, il va arrêter toutes les gouttes et aérosols qui s’en échapperaient (à condition d’être bien ajusté, le nez et la bouche à l'intérieur).
Si vous avez un masque vous êtes protégé(e) mais pas à 100%, mais si tout le monde porte un masque il n’y a pas de contamination, car il n’y a pas de goutte dans l’air.
Donc le masque doit être obligatoire en espace clos (où se trouve d’autres personnes dont on ne sait pas si elles sont saines), pour se protéger, mais surtout pour protéger les autres.En plein air, il n’y a pas de risque à être sans masque, à condition de respecter les distances d'un à 2 mètres avec les gens que l'on croise, mais, si vous voyez une personne qui tousse ou éternue, changez de trottoir.
Mais si vous rencontrez des amis et que vous parliez ensemble, mettez tous vos masques, le temps de la conversation.
Bien sûr, si personnes n’est malade dans votre famille, pas de masque dans votre maison.En ce qui concerne le masque que vous avez utilisé en espace clos, si personne n’a éternué ou toussé près de vous, il est peu probable qu’il soit contaminé. Vous pouvez donc le retirer par les élastiques le mettre dans un sac plastique et arrivé chez vous le suspendre par un clou à l’air et à la lumière. Les quelques virus qui pourraient y être meurent en 4 heures maximum et vous pouvez le remettre le lendemain.
Mais au total ne dépassez pas 8 heures de port, car ensuite il perd son efficacité.
Par contre, si quelqu’un a toussé ou éternué près de vous, une fois enlevé, jetez le ou lavez le en principe à 60 d°, mais à la machine à 40 d) avec toute la mousse du détergent, le virus morra par destruction des lipides de sa coque protectrice.Quand on regarde les causes des 95 foyers actuels de contamination, certes on trouve certains lieux où la distanciation n’a pas été respectée pendant le travail ou l’hébergement, comme les abattoirs ou les saisonniers en agriculture, mais on trouve des cas en entreprise où des réunions en espace clos ont pu entraîner une contamination et aussi des repas ou réunions lors de fêtes (mariages, anniversaires…), en particulier où l’on a mangé en discutant, nombreux autour d’une table, d’un apéritif ou de jeux. La parole peut être contagieuse, par les aérosols qui l’accompagnent.
 1 commentaire
1 commentaire
-
J'avais fait le 11 avril un article sur les modèles de prévision des épidémies. Mais ce n'était peut être pas assez clair car j'avais voulu trop simplifier et on m' demandé de faire un article plus complet.
Je le fais donc aujourd'hui, mais c'est un problème complexe et l'explication va être longue.
Les principaux renseignements que j'ai utilisés proviennent d’un article de Wikipédia (https://fr.wikipedia.org/wiki/Modèles_compartimentaux_en_épidémiologie) et d’une visio-conférence du Professeur Philippe Dumas (ENS Ulm, ancien directeur de Polytech Marseille)(https://cloud.cinam.univmrs.fr/owncloud/index.php/s/cKCTMduxPzgZO4O#pdfviewer) .
La propagation d’un agent infectieux au sein d’une population est un phénomène dynamique : les effectifs d’individus sains et malades évoluent dans le temps, en fonction des contacts au cours desquels cet agent passe d’un individu infecté à un individu sain non immunisé, l’infectant à son tour. Un tel phénomène peut être étudié en le modélisant par des équations et en déterminant son comportement à travers la résolution numérique de ces équations.
Les modèles mathématiques d’épidémies ont besoin de deux grand types de facteurs :
- Les caractéristiques de la population démographiques et géographiques : nombre, densité, type d’habitat, sexe, âge, structure familiale et ce qui est plus difficile à connaître les flux journaliers et les taux de contact entre personnes, très différents selon les régions, les lieux, les métiers et occupations de chacun, car dans une épidémie la transmission se fait souvent par contact ou cohabitation dans un même lieu, notamment de travail, une même pièce, un même moyen de transport.
- Les données sur la maladie que l’on peut représenter sur le graphique ci-
après :A noter que le temps de latence est celui à partir duquel on est contagieux, et qui peut être inférieur à l'incubation, qui est le temps au bout duquel apparaissent les symptômes de la maladie. Pour le Covid19, il semble que l'on puisse être contagieux 2 ou 3 jours avant l'apparition des symptômes, (s'il y en a, puisqu'il peut y avoir aussi des "porteurs sains").
Les modèles mathématiques pour prédire les épidémies sont donc très complexes et en général, organisés en "compartiments", dans lesquels on simule les phénomènes par des équations différentielles.
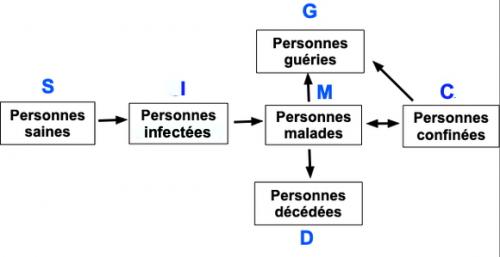
Dans le cas d'un virus comme le Covid19, dont les conséquences sont très variables, le compartiment des personnes malades peut être scindé en plusieurs sous-compartiments, tels "personnes à faibles symptômes", "malades à domicile", "personnes hospitalisées" et "personnes en réanimation". Il peut y avoir en outre des gens immunisés à la naissances ou vaccinéesLe but de la simulation est de calculer le nombre de personnes dans chaque compartiment, en fonction du temps S(t),(t), M(t) ....en fonction de paramètres qui régissent les variation de ces fonctions à chaque instant, lesquels dépendent des connaissances que l'on a de la maladie.
Pour simplifier on se limitera à un système à trois compartiments :
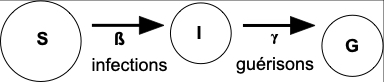
Parmi les personnes saines S d’une population de N membres, I personnes sont infectées, mais parmi elles, G malades guérissent.Les trois compartiments échangeant en permanence des flux.
Pour modéliser ces échanges, on définit deux paramètres :
- Une probabilité béta, ß, pour qu’une personne infectée rencontre dans la population de N membres, une personne saine et l’infecte.
La probabilité ß dépend de l’environnement : elle sera plus faible, en campagne que dans une ville, et plus forte dans un EPAD où les personnes sont confinées ou à fortiori sur un porte-avion ou un internat à dortoirs.
Une étude menée sur l’épidémie de covid19 dans le navire de croisière Diamond princess a montré qu’une personne en contaminait en moyenne 7, alors que dans la population, c’est un peu inférieur à 3.
- Une probabilité gamma, γ, pour qu’une personne infectée guérisse et redevienne donc saine.
Ces deux paramètres ne sont pas connus. On les fera varier pour connaître leur importance et se rapprocher des résultats expérimentaux, qui permettront de leur attribuer une valeur approximative..Au départ de l’épidémie, le nombre de personnes infectées I est faible et le nombre de personnes saines S est pratiquement égal à la population N.
A chaque instant dt, le nombre de personnes nouvellement infectées dI est égal à : dI = ß. I dt et S diminue de cette quantité dS = - ß.I dt
S diminue peu à peu et la probabilité ß ne s‘applique plus qu’à la proportion S/N donc dI = ß . S / N. I. dt
Mais il faut tenir compte des guérisons possibles dG = γ. I dt que l’on soustrait du chiffre des infectés et en définitive :
dI = dt (ß.S / N.I – γ.I) ce qui s’écrit aussi dI/I = dt . (ß.S / N. – γ.)
soit en intégrant Ln I = ∫(ß.S(t) / N. – γ.) dt = f(t) et I = e f(t)
Au début de l’épidémie, le nombre d’infections I va croître donc exponentiellement tant que (ß.S(t) / (N. – γ ) >0, c’et à dire S/N > γ / ß
Mais S diminuant, le nombre d’infection ralentit, passe par un maximum et lorsque S/N < γ / ß, le coefficient de l’exponentielle devient négatif et le nombre d’infection diminue de façon exponentielle, ce qui met fin au flux, une grande partie des personnes de la population ayant été contaminées successivement. Dans le cas du coronavirus, si ß = 3 et γ =1, le nombre maximal de personnes contaminées serait de ß / γ = 1 / 3. NLe rapport ß / γ est appelé R0. C’est en moyenne le rapport entre la probabilité de contamination en la probabilité de guérison. C’est en moyenne le nombre de personnes saines que peut contaminer une personne infectée.
Il y a donc un pic de contamination obtenu pour dI / dt = 0 et donc
S/N = γ / ß = 1 / Ro
Ceci en l’absence de mesures telles de confinement ou autres qui changeraient les divers facteurs.
Le confinement va diminuer la valeur de S, un nombre faible de personnes risquant alors d’être infecté.
L’amélioration des soins et de médicaments accroîtra la valeur du coefficient γ.
L’allure de la courbe pour ß = 0,3, γ= 0,1 et N = 100 000 est la suivante, sans mesure particulière pour lutter contre l’épidémie, qui se propage donc naturellement :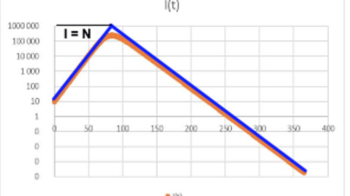 On remarquera que sur le graphique logarithmique, la partie exponentielle des courbes de montée et de descente de la valeur de I est très voisine de deux droites. (en bleu)
On remarquera que sur le graphique logarithmique, la partie exponentielle des courbes de montée et de descente de la valeur de I est très voisine de deux droites. (en bleu)
Ces deux droites sont une approximation des courbes de l’épidémie et se coupent en un point où I = N (alors que le max de I est de 1/R0 par rapport à N serait environ 1/3 pour le covid 19.)
La droite correspondant au développement de l’épidémie, passe par I0 = 10 pour t = 0 et par le point pour lequel I = N (100 000, et elle a une pente de dI/dt = ß.S(t) / N. –γ c’est à dire pour S = N de ß – γ
On peut donc calculer une approximation du temps du maximum
Ln (100 000) – Ln(10) = (ß – γ) ∆t d’où ∆t = (11,2 – 2,3) / (0,3-0,1) = 46 jours
La pente de la droite descendante est – gamma puisque elle est issue du point où I = N et qu’elle correspond donc à une absence de nouveaux cas et sa pente ne dépend donc plus que des guérisons et donc du coefficient gamma.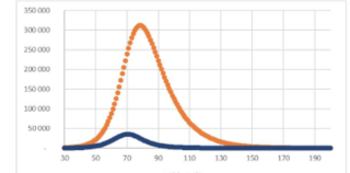 Il faut différencier deux pics :
Il faut différencier deux pics :- Celui du nombre total de personnes infectées i , (en rouge).
- Celui du nombre de nouvelles personnes infectées chaque jour dI / dt (en bleu).
Le pic des nouveaux infectés précède légèrement celui du nombre total d’infectés
Il faut toutefois se rendre compte que dans le modèle on compte toutes les personnes qui sont dans ces cas, alors que dans la réalité, il est difficile de les recenser, car certaines personnes ne se rendent pas compte qu’elle sont malades et ne consultent pas et il peut y avoir de porteurs sains. Dans le cas du coronavirus c’est un handicap, car cela peut représenter 20 à 30 % de la population.
Les valeurs que l’on a des coefficients ß et R0 sont donc approximatives et peuvent être assez variables selon l’environnement.Quelques R0 caractéristiques de maladies courantes :
Le modèle ci-dessus montre que si en France on restait face à la maladie sans rien faire, avec R0 = 3 on aurait un tiers de la population infectée, soit 20 millions.
Si 15% ont besoin de soins intensifs : --> 3 millions. Disponibles 10 000
Si 1/3 avec assistance respiratoire : --> 1 million . Disponibles 5 000
La mortalité même avec un chiffre bas de 3% ---> 600 000 mortsD’où la nécessité du confinement qui diminue la population qui peut être atteinte S et de « gestes barrières » qui diminuent la probabilité ß de contamination, (la probabilité de guérison γ restant fixe si les moyens de soins ne sont pas débordés par l’afflux de malades)
Isoler (par exemple en hôtel), les malades, qui ne sont pas gravement atteints, mais sont cependant contagieux, peut être aussi une mesure importante, car elle diminue fortement le contacts infectieux donc le coefficient ßEn ce qui concerne le confinement, un raisonnement simple permet de comprendre son effet sur le sombre de personnes S0 qui peuvent être contaminés:
Supposons qu’on soit au début de l’infection qu’il y ait environ 0,1% de personnes infectées. On a donc une chance sur mille d’être infecté .
Si on confine en coupant ces 60 millions de personnes en 12 millions de groupes de 5 personnes confinées. Il y a 5 pour mille de chances pour qu’une telle cellule soit infectée et donc 99,5 % de chances qu’elle ne soit pas infectée, ce qui représente donc un groupe à risque de 12 millions x 0,5 % = 60 000 personnes
On a donc fait passer la population à risque de S0 de 60 millions à 60 000, ce qui l’a divisé par 1000, ce qui permet de ramener les besoins sanitaires au-dessous des moyens existants, lorsque l’épidémie va se développer.
Certes un tel confinement total n’est pas possible, puisqu’il faut q’une partie des personnes travaille ou ayillent se ravitailler, mais cela permet de comprendre l’intérêt de l’opération.En définitive, le modèle ci-dessus à 3 compartiments est très simpliste, mais il permet de se rendre compte des principes de prévision, de sa difficulté aussi, car face à un nouveau virus, on ne connaît pas ses caractéristiques, et on obtient difficilement de chiffres du développement de l’épidémie (il est par exemple difficile de connaître le nombre exact de personnes infectées, en raison des cas asymptomatiques et des personnes faiblement atteintes, qui ne consultent pas un médecin.). Les paramètres sont donc difficiles à déterminer.
Par ailleurs les calculs faits sont plus complexes et ne sont pas littéraux, mais on fait des simulations. Dans le cas ci-dessus des trois compartiments, on serait par exemple parti d’une hypothèse de valeur des paramètres ß et γ, et d’un I0 par exemple de 10 et on aurait demandé à l’ordinateur, de calculer chaque jour la valeur du nombre d’infectés I, de la population restante S et du nombre de guéris G. L’ordinateur trace ensuite les courbes en fonction du temps, que l’on compare à la réalité. On prend une autre valeur des paramètres et on regarde si elle est plus proche du réel.
Dans le cas du covid19, étant donné la difficulté pour avoir des valeurs réelles de I, il est nécessaire de traiter davantage de compartiments car les seuls chiffres sûrs sont les entrées à l’hôpital, les mises en réanimation et les décès.
Mais le modèle simple à 3 compartiments permet de se rendre compte de la gravité de la propagation du virus si aucune mesure n’est prise, et de la conséquence inexorable alors, du débordement des moyens sanitaires. votre commentaire
votre commentaire
-
L'Université Johns-Hopkins de Baltimore est depuis 1878, une université très connue américaine, qui comporte notamment une faculté de médecine prestigieuse, qui fait enseignement et recherche, et, comme beaucoup d'universités américaines, entretient des liens étroits avec les hôpitaux. Elle doit son nom à Johns Hopkins, un riche industriel qui a légué à sa mort 7 millions de $ à l'université.et elle possède des campus à Washington, à Bologne en Italie, à Singapour et à Nankin en Chine.
Elle s'intéresse évidemment à la pandémie de Covid-19 et notamment tient en permanence une carte interactive qui dénombre en temps réel les personnes ayant été testées positives ou mortes des suites du Covid-19 dans le monde, et recherche un vaccin contre ce virus, qu'elle espère mettre au point d'ici un an à 18 mois.
Un de ses chercheurs a rédigé un texte sur les gestes de protection contre le coronavirus, remarquable par sa simplicité et sa clarté. En voici, ci-après, une traduction, qui mérite d'être diffusée, car elle peut être utile à bon nombre de personnes :
* Le virus n'est pas un organisme vivant, mais un assemblage de protéines et d'ADN, recouvert d'une couche protectrice de lipides (graisses) qui, lorsqu'elle est absorbée par les cellules des muqueuses oculaires, nasales ou buccales, modifie leur code génétique et les convertit en cellules qui multiplient le virus, lequel va ensuite envahir les poumons.
* Parce que le virus n'est pas un organisme vivant mais une molécule de protéines, il n'est pas tué, mais se décompose de lui-même. Le temps de désintégration dépend de la température, de l'humidité et du type de matériau dans lequel il se trouve.
* Le virus est très fragile ; la seule chose qui le protège est une fine couche de graisse extérieure. C'est pourquoi tout savon ou détergent est le meilleur remède, car la mousse détruit les graisses (c'est pourquoi il faut frotter autant : pendant au moins 20 secondes ou plus, et faire beaucoup de mousse). En dissolvant la couche de graisse, l'assemblage de protéines se disperse et se décompose de lui-même.
* La chaleur dissout la graisse ; utilisez de l'eau à une température supérieure à 25 degrés pour vous laver les mains, les vêtements et tout le reste. De plus, l'eau chaude produit plus de mousse, ce qui la rend encore plus utile.
* L'alcool ou tout mélange avec de l'alcool à plus de 65% dissout les graisses , en particulier la couche lipidique externe du virus.
* Tout mélange avec 1 partie d'eau de javel et 5 parties d'eau dissout directement la protéine, la décomposant de l'intérieur (mais cela abîme les mains).
* L'eau oxygénée (peroxyde d'hydrogène), aide beaucoup après le savon, l'alcool et le chlore, car le peroxyde dissout la protéine virale, mais il faut l'utiliser pure et elle fait mal à la peau.
* Pas de bactéricides ! Le virus n'est pas un organisme vivant comme les bactéries ; on ne peut pas tuer ce qui n'est pas vivant avec des antibiotiques, mais désintégrer rapidement sa structure avec tout ce qui a été dit.
* NE JAMAIS secouer les vêtements, draps qui risquent d'être contaminés. Bien que collé sur une surface poreuse, le virus est inerte et se désintègre en 3 heures (tissu et poreux), 4 heures (cuivre, car il est naturellement antiseptique ; et bois, car il élimine toute humidité), 24 heures (carton), 42 heures (métal) et 72 heures (plastique). Mais si vous le secouez ou utilisez un chiffon, les molécules du virus flottent dans l'air pendant 3 heures et peuvent se déposer dans votre nez.
* Les molécules virales restent très stables dans le froid extérieur ou artificiel comme les climatiseurs des maisons et des voitures et les réfrigérateurs. Ils ont également besoin d'humidité pour rester stables et surtout de l'obscurité. Par conséquent, les environnements déshumidifiés, secs, chauds et lumineux les dégraderont plus rapidement.
* La lumière UV sur tout objet brisera la protéine du virus. Par exemple, pour désinfecter et réutiliser un masque c’est parfait. Attention, il décompose également le collagène (qui est une protéine) de la peau, ce qui finit par provoquer des rides et le cancer de la peau (si c'est à long terme).
* Le virus ne peut PAS passer à travers une peau saine.
* Le vinaigre n'est PAS utile car il ne décompose pas la couche protectrice de graisse.
* Pas d'alcool comestible (whisky, vodka...)La vodka la plus forte est à 40 % d'alcool. Il en faut 65 % et plus pour détruire le virus.
* Plus l'espace est limité, plus la concentration du virus est importante. Plus ouvert ou ventilé naturellement sera l’espace, moins il sera concentré. Ne fermez pas les ventilations.
* Ceci étant dit, voilà pourquoi vous devez vous laver les mains avant et après avoir touché des muqueuses, de la nourriture, des serrures, des boutons, des interrupteurs, une télécommande, un téléphone portable, des montres, un ordinateur, des bureaux, une télévision, etc. et quand on utilise les toilettes.
* Il faut aussi s'humidifier les mains, par exemple en les lavant beaucoup, car les molécules peuvent se cacher dans des micro-rides ou les coupures. Plus l'hydratant est épais, mieux c'est.
* Gardez même les ongles courts pour que le virus ne s'y cache pas. votre commentaire
votre commentaire
-
Depuis le début de l'épidémie de coronavirus, on nous parle des prévisions concernant son évolution faites par des scientifiques qui conseillent le gouvernement. Mais que sont donc les modèles mathématiques qui servent pour ces prévisions.
J'ai donc pensé que cela vous intéresserait peut être de comprendre comment cela fonctionnait et j'ai donc lu plusieurs articles d'explications, avec beaucoup de mal d'ailleurs, car les mathématiques ont beaucoup évolué depuis mes études d'ingénieur, notamment grâce aux résolutions des équations sur ordinateur.
Rassurez vous, je vais essayer d'être simple et je ne vais pas vous embarquez dans des équations compliquées : je me limiterai aux principes.Mais d'abord, qu’est ce qu’un modèle mathématique ? et une simulation ?
Quand vous prenez votre voiture pour partir en vacances et que vous roulez sur l’autoroute à vitesse constante, vous savez que la distance d que vous parcourez pendant un temps donné, est le produit de votre vitesse v par le temps t.
Dire que d = v t est un modèle mathématique est un peu abusif, tant c’est simplifié à l’état d’une simple formule qu’on apprend en CM1, mais c’est un exemple.
En effet on est parti de la réalité, on a fait des mesures de distance, vitesse et temps et on a abouti à cette équation toute simple. On est allé de l’expérience aux mathématiques. Ensuite si on connaît sa vitesse on peut calculer les distances parcourues à diverses heures; On se sert de la formule mathématique pour prévoir la situation.
Un modèle mathématique est analogue, si ce n’est que les équations sont beaucoup plus compliquées et cela d’autant plus que les phénomènes sont complexes.
Cela concerne en général un phénomène physique, chimique ou biologique; on part d’observations numériques et d’hypothèses d’équations issues d’une explication scientifique du phénomène, on bâtit un modèle à base de ces équations, et ensuite on essaie de prévoir les résultats d’expériences que l’on peut faire sur le phénomène. On peut alors vérifier si les résultats des mesures sont conformes à ceux prévus par le modèle ou s’il faut modifier celui-ci, soit en changeant les équations, soit en ajustant des paramètres dans les équations utilisées.
On peut ensuite utiliser ces modèles mathématiques pour prévoir des phénomènes analogues, mais qui ne sont pas encore arrivés, et pour établir diverses situations en fonctions d’hypothèses de départ initiales différentes. C’est ce qu’on appelle une simulation. C’est par exemple ce que l’on essaye de faire en simulant les conséquences sur le climat, de la production des gaz à effet de serre ou la progression de l'épidémie de coronavirus.
Un petit complément au cas où vous entendriez ces mots :
Certains modèles sont dits « déterministes » : c’était le cas de notre voiture. Ce sont des modèles où on décompose les phénomènes en étapes successives et où on peut expliciter les événements par des données initiales, des équations qui représentent le phénomène de façon supposée exacte, et où on aboutit à des données finales, cela sans intervention des lois de probabilité. Cela suppose en quelque sorte que les phénomènes sont déterminés, c’est à dire qu’ils se passent toujours de la même façon.
A l’inverse il y a des phénomènes que l’on est incapable de décrire par des données et des équations permanentes et où donc les éléments ne se comportent pas toujours de la même façon. Par contre on peut observer une certaine répartition statistique des comportements. On peut alors se servir des calculs mathématiques des probabilités pour décrire ces phénomènes. On parle alors de modèles « stochastiques »
On a enfin des cas où les phénomènes dépendent d’une multitude de petites causes et on n’est jamais certain de les connaître toutes et de pouvoir les quantifier.
On dit alors qu’ils se produisent « au hasard » et on simule mathématiquement ce hasard.
Bien entendu de tels calculs étaient très difficiles à faire quand j’ai fait mes études (à la main avec des tables de logarithmes, que la plupart d’entre vous n’ont jamais connues). Aujourd’hui, tout se fait évidemment sur ordinateur et des simulations complexes comme celles sur le climat, ou le Covid19 demandent des ordinateurs très puissants.
Mais vous constatez donc que pour faire un « modèle mathématique » il ne suffit pas d’être matheux, il faut en outre bien connaître le phénomène scientifique que l’on veut simuler. Donc dans le cas des épidémies, il faut d’abord voir ce qu’on doit connaître sur ce sujet. Et ensuite il faut avoir de nombreux chiffres constatant l'évolution réelle des phénomènes. C’est ce que je vais essayer de vous montrer.La propagation d’un agent infectieux au sein d’une population est un phénomène dynamique : les effectifs d’individus sains et malades évoluent dans le temps, en fonction des contacts au cours desquels cet agent passe d’un individu infecté à un individu sain non immunisé, l’infectant à son tour. Un tel phénomène peut être étudié en le modélisant par des équations et en déterminant son comportement à travers la résolution numérique de ces équations.
Les modèles mathématiques d’épidémies ont besoin de deux grand types de facteurs :
- Les caractéristiques de la population démographiques et géographiques : nombre, densité, type d’habitat, sexe, âge, structure familiale et ce qui est plus difficile à connaître les flux journaliers et les taux de contact entre personnes, très différents selon les métiers et occupations de chacun, car dans une épidémie la transmission se fait souvent par contact ou cohabitation dans un même lieu, notamment de travail, une même pièce, un même moyen de transport.
- Les données sur la maladie que l’on peut représenter sur le graphique ci dessous :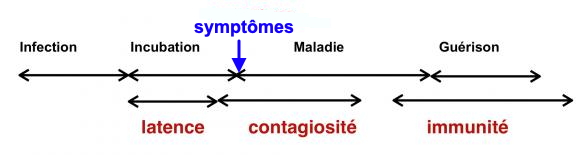
A noter que le temps de latence est celui à partir duquel on est contagieux, et qui peut être inférieur à l'incubation, qui est le temps au bout duquel apparaissent les symptômes de la maladie. Pour le Covid19, il semble que l'on puisse être contagieux 2 ou 3 jours avant l'apparition des symptômes, (s'il y en a puisqu'il peut y avoir aussi des "porteurs sains").
On pourrait utiliser des modèles simples comme les deux suivants :
- Si l'on ne fait rien et qu'une personne en contamine 3 en moyenne dans un espace de temps ∆t, le nombre de personnes malades croit chaque ∆t comme ", 32, 33...3n.. c'est à dire comme une courbe exponentielle. Effectivement les courbes d'expansion du coronavirus ont cette allure, mais la valeur de ce coefficient n'est pas connue et varie selon les circons-tances et donc un modèle aussi simple, calculable sur Excel, est aberrant.
- On pourrait penser que le nombre de personnes infectées dans une durée donnée Ni est proportionnel au nombre d’individus sains S, au taux de contact c, à la probabilité p que ce contact ait lieu avec une personne infectée et à une probabilité de transmission de la maladie m : Ni (t) = S x c x p x m, t étant le temps. Mais ces paramètres ne sont pas non plus connus.Les modèles mathématiques pour prédire les épidémies sont donc beaucoup plus complexes et en général, organisés en "compartiments", dans lesquels on simule les phénomènes par des équations différentielles.
Dans le cas d'un virus comme le Covid19, dont les conséquences sont très variables, le compartiment des personnes malades peut être scindé en plusieurs sous-compartiments, tels "personnes à faibles symptômes", "malades à domicile", "personnes hospitalisées" et "personnes en réanimation".
Le but de la simulation est de calculer le nombre de personnes dans chaque compartiment, en fonction du temps S(t), C(t), M(t) ....en fonction de paramètres qui régissent les variation dS/dt, dC/dt, dM/dt ... de ces fonctions à chaque instant.
Ces paramètres dépendent des connaissances que l'on a de la maladie.On a donc une série d'équations différentielles que l'on peut résoudre sur ordinateur, en affectant des valeurs à ces paramètres. On compare alors les chiffres calculés à la réalité de ceux obtenus sur le terrain tous les jours, et on modifie la valeur des paramètres pour que la correspondance soit la meilleure possible.
Mais mettre sur pied une simulation fiable n'est pas simple, car il faut avoir des chiffres corrects de la réalité, et par exemple cela n'est pas le cas en France pour le coronavirus, pour le nombre de contaminés, puisque les tests ne permettent pas de le connaître. On ne peut se baser que sur des chiffres de personnes atteintes nettement, hospitalisées ou en réanimation. De plus il peut y avoir des variations de ces coefficients dans le temps : par exemple l'infectiosité d'un individu peut varier en fonction de l'avancement de la maladie, la quantité de virus ingérée par un individu est variable selon les circonstances de la contamination, le virus peut muter....
De plus une telle simulation peut être faite pour tout le pays et la population entière, mais aussi pour une région donnée (par exemple Alsace ou Ile de France), ou pour une tranche d'âges de la population.
Mais les populations ne sont pas non plus homogènes, ne serait ce que parce que les conditions de vie ne sont pas lés mêmes, les états de santé hors épidémie étudiée, sont différents et les sensibilités des individus à l'épidémie en cause sont aussi très différentes, tout particulièrement en ce qui concerne le coronavirus actuel.
On pourrait aussi ajouter un compartiment pour étudier l'influence d'un médicament, ou d'une mesure, si elle est appliquée à un grand nombre de personnes. (pour étudier l'influence d'un médicament sur quelques personnes, on peut suivre des paramètres biologiques précis).De tels modèles ne peuvent donc avoir une très grande précision et notamment lorsque le virus est nouveau et peu connu, mais ils permettent d'avoir une idée approximative de l'influence de certaines mesures de protection ou de la charge des moyens de santé, et ils sont donc une aide à la décision des personnes qui gèrent la crise sanitaire.
 1 commentaire
1 commentaire
-
La photo ci dessus rest celle d'un superbe château de sable, réalisé sur une plage de Bretagne, lors d'un concours. Mais un château de sable, c'est fragile et la pluie ou la marée vont le détruire hélas. Faut il désespérer de cette catastrophe ?
Le 3 mars 2019, j'avais publié et commenté l'exercice codé suivant que je réédite ci-dessous pour vous amuser, mais j'en donne tout de suite la traduction, car ce texte est important pour moi.
> > > UN B34U JOUR D'373,
> > > J'37415 5UR L4 PL4G3 37 J3 R3G4RD415 D3UX J3UN35 F1LL35 JOU4N7 D4N5 L3 54BL3. 3LL35 CON57RU15413N7 UN CHÂ734U D3 54BL3, 4V3C 7OUR5, P4554G35 C4CH35 37 PON7-L3V15. 4LOR5 QU'3LL35 73RM1N413N7, UN3 V4GU3 357 4RR1V33 37 4 7OU7 D37RU17, R3DU154N7 L3 CH4734U 3N UN 745 D3 54BL3 37 D'3CUM3.J'41 CRU QU'4PR35 74N7 D'3FFOR7, L35 F1LL37735 COM3NÇ3R413N7 4 PL3UR3R, M415 4U CON7R41R3 3LL35 COURRUR3N7 5UR L4 PL4G3, R14N7 37 JOU4N7 37 COMM3NÇ3R3N7 4 CON57RU1R3 UN 4U7R3 CHÂ734U. J'41 COMPR15 QU3 J3 V3N415 D'4PPR3NDR3 UN3 GR4ND3 L3ÇON. NOU5 P455ON5 UN3 GR4ND3 P4R713 D3 NO7R3 V13 4 CON57RU1R3 D35 CHO535 M415 LOR5QU3 PLU5 74RD UN3 V4GU3 L35 D3MOL17, L35 53UL35 CHO535 QU1 R3573N7 5ON7 L'4M1713, L'4MOUR 37 L '4FF3C71ON 37 L35 M41N5 D35 G3N5 QU1 5ON7 C4P4BL35 D3 NOU5 F41R3 5OUR1R3.“....J'étais sur la plage et je regardais deux petites filles jouant dans le sable. Elles construisaient un château de sable, avec tours, passages secrets et pont-levis. Alors qu'elles terminaient, une vague est arrivée et a tout détruit, réduisant le château en un tas de sable et d'écume.
J'ai cru qu'après tant d'efforts, les fillettes commençeraient à pleurer, mais au contraire elles courrurent sur la plage, riant et jouant et commencèrent à construire un autre château.
J'ai compris que je venais d'apprendre une grande leçon. Nous passons une grande partie de notre vie à construire des choses, mais lorsque, plus tard, une vague les démolit, les seules choses qui restent sont l'amitié, l'amour et l'affection et les gens qui sont capables de nous faire sourire. “L'attitude de ces enfants est pour moi un exemple, et un message que j’essaie souvent de faire passer auprès des jeunes qui m’écrivent et qui traversent un mauvais passage dans leur vie, parce quelque chose ou quelqu’un auquel ils tenaient beaucoup vient de sortir de leur existence.
Il faut alors s’occuper pour penser à autre chose, travailler le mieux possible : reconstruire un autre château de sable.
Et puis il faut s’appuyer sur les amis, sur la famille, pour faire des choses ensemble, se changer l’esprit, rire à nouveau.`
Bien sûr on a envie de pleurer, mais il faut surmonter cette envie. Rester dans son coin à le faire ne sert à rien, si ce n’est à faire tourner les pensées tristes dans votre cerveau et à stresser encore plus.
Certes c’est dur de tourner la page, d’oublier le passé, de ne pas se reprocher ses erreurs, mais cela sert à quoi de ressasser tout cela sinon à être encore plus mal.
Il faut changer de registre, rêver à nouveau, refaire des projets réalistes à partir de ses rêves, et se donner les moyens de les réaliser avec motivation et volonté.
A deux reprises, dans ma jeunesse,”la mer a détruit mon château de sable” et je vous assure que le seul moyen d’en sortir c’est d’avaler ses larmes, de serrer les dents et de repasser à l’action, d’essayer de le reconstruire, avec l’aide de la famille et des amis.
Et parfois on trouve aussi, à la fin, un nouvel amour, une nouvelle passion.Je ferai demain un article sur la dépression. Bien entendu lorsqu'on est vraiment en dépression, il faut aller voir un médecin et se faire soigner, car c'est un dérèglement de l'organisme et du cerveau, et donc c'est analogue à une maladie. Et les médicaments que prescrit le médecin sont alors nécessaires.
Mais la plupart du temps, malgré de grands chagrins nous ne sommes pas en dépression. Nous traversons seulement une mauvaise passe, nous sommes stressés, anxieux. Depuis plus de 15 ans que je suis sur mes blogs successifs, j'ai aidé plus d'une centaine de jeunes qui se trouvaient dans cette situation.
Beaucoup d'entre eux se sentaient mal, l'esprit vide et ressassaient des idées tristes, mais sauf s'ils avaient subi un traumatisme particulier et avéré, ils ne savaient pas me dire pourquoi ils se sentaient ainsi diminués, incapables d'agir efficacement.
La première chose à faire dans ce cas, c'est d'examiner son environnement, le déroule-ment de sa vie, ce qui s'est passé récemment, nos rapports avec d'autres, bref essayer de trouver ce qui s'est mal passé, quel est le château de sable qui s'est détruit ou menace de s'écrouler, quel est la ou les causes de notre mal-être.
On pourrait croire que c'est facile. Eh bien non ! Notre cerveau essaie de nous défendre contre ces éléments qui nous blessent et pour cela il nous les occulte, il essaie de nous les faire oublier. Ils sont dans notre inconscient, bien cachés et il faut réfléchir pour les trouver, les traquer avec logique et bon sens, un peu comme dans une enquête policière.
Et souvent, nous ne voulons pas voir ces causes, parce qu'elles nous dérangent, que nous avons des sentiments divers vis à vis d'elles, comme la culpabilité par exemple. Et puis nous avons des émotions, des sentiments et donc nous ne sommes pas insensibles devant ces causes, et cela nous empêche souvent de les traiter logiquement, froidement , en "spectateur".
C'est pour cela que dans ces situations on a besoin souvent que quelqu'un vous aide, reprenne avec vous les causes possibles, vous aide à les analyser objectivement et à faire la part des choses, la recherche des raisons de votre mal être.
Une fois les causes trouvées, on peut alors examiner la situation, tirer les leçons du passé et tourner la page, examiner le présent et l'avenir, chercher les remèdes, réparer ce qui est possible et sinon se reconstruire, refaire un nouveau château de sable.C'est déjà difficile pour un adulte, cela l'est encore plus pour un ado, car il est encore fragile, qu'il veut rester dans l'enfance dans le présent, à l'abri du nid familial, mais doit aussi se projeter dans l'avenir et devenir capable de voler de ses propres ailes et de conquérir l'indépendance et la responsabilité de sa vie future. C'est là où les conseil d'un ancien peuvent lui suggérer des images d'un avenir possible, qu'il n'imagine pas facilement, car il n'en a pas encore l'expérience.
 1 commentaire
1 commentaire Suivre le flux RSS des articles
Suivre le flux RSS des articles Suivre le flux RSS des commentaires
Suivre le flux RSS des commentaires