-
Les modèles mathématiques de simulation des épidémies.
Depuis le début de l'épidémie de coronavirus, on nous parle des prévisions concernant son évolution faites par des scientifiques qui conseillent le gouvernement. Mais que sont donc les modèles mathématiques qui servent pour ces prévisions.
J'ai donc pensé que cela vous intéresserait peut être de comprendre comment cela fonctionnait et j'ai donc lu plusieurs articles d'explications, avec beaucoup de mal d'ailleurs, car les mathématiques ont beaucoup évolué depuis mes études d'ingénieur, notamment grâce aux résolutions des équations sur ordinateur.
Rassurez vous, je vais essayer d'être simple et je ne vais pas vous embarquez dans des équations compliquées : je me limiterai aux principes.Mais d'abord, qu’est ce qu’un modèle mathématique ? et une simulation ?
Quand vous prenez votre voiture pour partir en vacances et que vous roulez sur l’autoroute à vitesse constante, vous savez que la distance d que vous parcourez pendant un temps donné, est le produit de votre vitesse v par le temps t.
Dire que d = v t est un modèle mathématique est un peu abusif, tant c’est simplifié à l’état d’une simple formule qu’on apprend en CM1, mais c’est un exemple.
En effet on est parti de la réalité, on a fait des mesures de distance, vitesse et temps et on a abouti à cette équation toute simple. On est allé de l’expérience aux mathématiques. Ensuite si on connaît sa vitesse on peut calculer les distances parcourues à diverses heures; On se sert de la formule mathématique pour prévoir la situation.
Un modèle mathématique est analogue, si ce n’est que les équations sont beaucoup plus compliquées et cela d’autant plus que les phénomènes sont complexes.
Cela concerne en général un phénomène physique, chimique ou biologique; on part d’observations numériques et d’hypothèses d’équations issues d’une explication scientifique du phénomène, on bâtit un modèle à base de ces équations, et ensuite on essaie de prévoir les résultats d’expériences que l’on peut faire sur le phénomène. On peut alors vérifier si les résultats des mesures sont conformes à ceux prévus par le modèle ou s’il faut modifier celui-ci, soit en changeant les équations, soit en ajustant des paramètres dans les équations utilisées.
On peut ensuite utiliser ces modèles mathématiques pour prévoir des phénomènes analogues, mais qui ne sont pas encore arrivés, et pour établir diverses situations en fonctions d’hypothèses de départ initiales différentes. C’est ce qu’on appelle une simulation. C’est par exemple ce que l’on essaye de faire en simulant les conséquences sur le climat, de la production des gaz à effet de serre ou la progression de l'épidémie de coronavirus.
Un petit complément au cas où vous entendriez ces mots :
Certains modèles sont dits « déterministes » : c’était le cas de notre voiture. Ce sont des modèles où on décompose les phénomènes en étapes successives et où on peut expliciter les événements par des données initiales, des équations qui représentent le phénomène de façon supposée exacte, et où on aboutit à des données finales, cela sans intervention des lois de probabilité. Cela suppose en quelque sorte que les phénomènes sont déterminés, c’est à dire qu’ils se passent toujours de la même façon.
A l’inverse il y a des phénomènes que l’on est incapable de décrire par des données et des équations permanentes et où donc les éléments ne se comportent pas toujours de la même façon. Par contre on peut observer une certaine répartition statistique des comportements. On peut alors se servir des calculs mathématiques des probabilités pour décrire ces phénomènes. On parle alors de modèles « stochastiques »
On a enfin des cas où les phénomènes dépendent d’une multitude de petites causes et on n’est jamais certain de les connaître toutes et de pouvoir les quantifier.
On dit alors qu’ils se produisent « au hasard » et on simule mathématiquement ce hasard.
Bien entendu de tels calculs étaient très difficiles à faire quand j’ai fait mes études (à la main avec des tables de logarithmes, que la plupart d’entre vous n’ont jamais connues). Aujourd’hui, tout se fait évidemment sur ordinateur et des simulations complexes comme celles sur le climat, ou le Covid19 demandent des ordinateurs très puissants.
Mais vous constatez donc que pour faire un « modèle mathématique » il ne suffit pas d’être matheux, il faut en outre bien connaître le phénomène scientifique que l’on veut simuler. Donc dans le cas des épidémies, il faut d’abord voir ce qu’on doit connaître sur ce sujet. Et ensuite il faut avoir de nombreux chiffres constatant l'évolution réelle des phénomènes. C’est ce que je vais essayer de vous montrer.La propagation d’un agent infectieux au sein d’une population est un phénomène dynamique : les effectifs d’individus sains et malades évoluent dans le temps, en fonction des contacts au cours desquels cet agent passe d’un individu infecté à un individu sain non immunisé, l’infectant à son tour. Un tel phénomène peut être étudié en le modélisant par des équations et en déterminant son comportement à travers la résolution numérique de ces équations.
Les modèles mathématiques d’épidémies ont besoin de deux grand types de facteurs :
- Les caractéristiques de la population démographiques et géographiques : nombre, densité, type d’habitat, sexe, âge, structure familiale et ce qui est plus difficile à connaître les flux journaliers et les taux de contact entre personnes, très différents selon les métiers et occupations de chacun, car dans une épidémie la transmission se fait souvent par contact ou cohabitation dans un même lieu, notamment de travail, une même pièce, un même moyen de transport.
- Les données sur la maladie que l’on peut représenter sur le graphique ci dessous :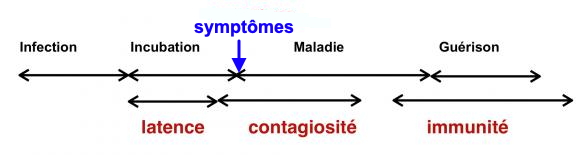
A noter que le temps de latence est celui à partir duquel on est contagieux, et qui peut être inférieur à l'incubation, qui est le temps au bout duquel apparaissent les symptômes de la maladie. Pour le Covid19, il semble que l'on puisse être contagieux 2 ou 3 jours avant l'apparition des symptômes, (s'il y en a puisqu'il peut y avoir aussi des "porteurs sains").
On pourrait utiliser des modèles simples comme les deux suivants :
- Si l'on ne fait rien et qu'une personne en contamine 3 en moyenne dans un espace de temps ∆t, le nombre de personnes malades croit chaque ∆t comme ", 32, 33...3n.. c'est à dire comme une courbe exponentielle. Effectivement les courbes d'expansion du coronavirus ont cette allure, mais la valeur de ce coefficient n'est pas connue et varie selon les circons-tances et donc un modèle aussi simple, calculable sur Excel, est aberrant.
- On pourrait penser que le nombre de personnes infectées dans une durée donnée Ni est proportionnel au nombre d’individus sains S, au taux de contact c, à la probabilité p que ce contact ait lieu avec une personne infectée et à une probabilité de transmission de la maladie m : Ni (t) = S x c x p x m, t étant le temps. Mais ces paramètres ne sont pas non plus connus.Les modèles mathématiques pour prédire les épidémies sont donc beaucoup plus complexes et en général, organisés en "compartiments", dans lesquels on simule les phénomènes par des équations différentielles.
Dans le cas d'un virus comme le Covid19, dont les conséquences sont très variables, le compartiment des personnes malades peut être scindé en plusieurs sous-compartiments, tels "personnes à faibles symptômes", "malades à domicile", "personnes hospitalisées" et "personnes en réanimation".
Le but de la simulation est de calculer le nombre de personnes dans chaque compartiment, en fonction du temps S(t), C(t), M(t) ....en fonction de paramètres qui régissent les variation dS/dt, dC/dt, dM/dt ... de ces fonctions à chaque instant.
Ces paramètres dépendent des connaissances que l'on a de la maladie.On a donc une série d'équations différentielles que l'on peut résoudre sur ordinateur, en affectant des valeurs à ces paramètres. On compare alors les chiffres calculés à la réalité de ceux obtenus sur le terrain tous les jours, et on modifie la valeur des paramètres pour que la correspondance soit la meilleure possible.
Mais mettre sur pied une simulation fiable n'est pas simple, car il faut avoir des chiffres corrects de la réalité, et par exemple cela n'est pas le cas en France pour le coronavirus, pour le nombre de contaminés, puisque les tests ne permettent pas de le connaître. On ne peut se baser que sur des chiffres de personnes atteintes nettement, hospitalisées ou en réanimation. De plus il peut y avoir des variations de ces coefficients dans le temps : par exemple l'infectiosité d'un individu peut varier en fonction de l'avancement de la maladie, la quantité de virus ingérée par un individu est variable selon les circonstances de la contamination, le virus peut muter....
De plus une telle simulation peut être faite pour tout le pays et la population entière, mais aussi pour une région donnée (par exemple Alsace ou Ile de France), ou pour une tranche d'âges de la population.
Mais les populations ne sont pas non plus homogènes, ne serait ce que parce que les conditions de vie ne sont pas lés mêmes, les états de santé hors épidémie étudiée, sont différents et les sensibilités des individus à l'épidémie en cause sont aussi très différentes, tout particulièrement en ce qui concerne le coronavirus actuel.
On pourrait aussi ajouter un compartiment pour étudier l'influence d'un médicament, ou d'une mesure, si elle est appliquée à un grand nombre de personnes. (pour étudier l'influence d'un médicament sur quelques personnes, on peut suivre des paramètres biologiques précis).De tels modèles ne peuvent donc avoir une très grande précision et notamment lorsque le virus est nouveau et peu connu, mais ils permettent d'avoir une idée approximative de l'influence de certaines mesures de protection ou de la charge des moyens de santé, et ils sont donc une aide à la décision des personnes qui gèrent la crise sanitaire.
-
Commentaires



Et bin dit donc grâce à toi je vais être plus forte que mon frère!